Generalized Linear Models¶
Generalized linear models currently supports estimation using the one-parameter exponential families.
See Module Reference for commands and arguments.
Examples¶
# Load modules and data
In [1]: import statsmodels.api as sm
In [2]: data = sm.datasets.scotland.load()
In [3]: data.exog = sm.add_constant(data.exog)
# Instantiate a gamma family model with the default link function.
In [4]: gamma_model = sm.GLM(data.endog, data.exog, family=sm.families.Gamma())
In [5]: gamma_results = gamma_model.fit()
In [6]: print(gamma_results.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 32
Model: GLM Df Residuals: 24
Model Family: Gamma Df Model: 7
Link Function: inverse_power Scale: 0.00358428317349
Method: IRLS Log-Likelihood: -83.017
Date: Tue, 28 Feb 2017 Deviance: 0.087389
Time: 21:38:03 Pearson chi2: 0.0860
No. Iterations: 4
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0178 0.011 -1.548 0.122 -0.040 0.005
x1 4.962e-05 1.62e-05 3.060 0.002 1.78e-05 8.14e-05
x2 0.0020 0.001 3.824 0.000 0.001 0.003
x3 -7.181e-05 2.71e-05 -2.648 0.008 -0.000 -1.87e-05
x4 0.0001 4.06e-05 2.757 0.006 3.23e-05 0.000
x5 -1.468e-07 1.24e-07 -1.187 0.235 -3.89e-07 9.56e-08
x6 -0.0005 0.000 -2.159 0.031 -0.001 -4.78e-05
x7 -2.427e-06 7.46e-07 -3.253 0.001 -3.89e-06 -9.65e-07
==============================================================================
Detailed examples can be found here:
Technical Documentation¶
The statistical model for each observation  is assumed to be
is assumed to be
and
.
where  is the link function and
is the link function and  is a distribution of the family of exponential dispersion models (EDM) with
natural parameter
is a distribution of the family of exponential dispersion models (EDM) with
natural parameter  , scale parameter
, scale parameter 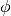 and weight
and weight
 .
Its density is given by
.
Its density is given by
It follows that  and
and
![Var[Y|x]=\frac{\phi}{w}b''(\theta)](_images/math/d89edf7a8bb1e6e8b774af2f77ed05cd585a03d3.png) . The inverse of the first equation
gives the natural parameter as a function of the expected value
. The inverse of the first equation
gives the natural parameter as a function of the expected value
 such that
such that
with  . Therefore it is said that a GLM is
determined by link function
. Therefore it is said that a GLM is
determined by link function  and variance function
and variance function  alone (and
alone (and 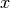 of course).
of course).
Note that while 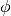 is the same for every observation
is the same for every observation  and therefore does not influence the estimation of
and therefore does not influence the estimation of  ,
the weights
,
the weights  might be different for every
might be different for every  such that the
estimation of
such that the
estimation of  depends on them.
depends on them.
| Distribution | Domain | ![\mu=E[Y|x]](_images/math/fdff08089137d887b7e63a434315206a7be7cd76.png) |
 |
 |
 |
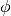 |
|---|---|---|---|---|---|---|
Binomial  |
 |
 |
 |
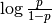 |
 |
1 |
Poisson 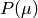 |
 |
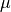 |
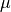 |
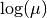 |
 |
1 |
Neg. Binom.  |
 |
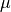 |
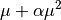 |
 |
 |
1 |
Gaussian/Normal  |
 |
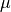 |
 |
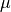 |
 |
 |
Gamma  |
 |
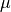 |
 |
 |
 |
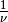 |
Inv. Gauss.  |
 |
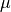 |
 |
 |
 |
 |
Tweedie  |
depends on 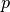 |
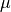 |
 |
 |
 |
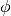 |
The Tweedie distribution has special cases for 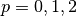 not listed in the
table and uses
not listed in the
table and uses  .
.
Correspondence of mathematical variables to code:
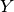 and
and 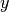 are coded as
are coded as endog, the variable one wants to model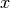 is coded as
is coded as exog, the covariates alias explanatory variables is coded as
is coded as params, the parameters one wants to estimate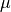 is coded as
is coded as mu, the expectation (conditional on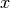 )
of
)
of 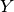
 is coded as
is coded as linkargument to theclass Family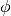 is coded as
is coded as scale, the dispersion parameter of the EDM is not yet supported (i.e.
is not yet supported (i.e.  ), in the future it might be
), in the future it might be
var_weights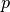 is coded as
is coded as var_powerfor the power of the variance function of the Tweedie distribution, see table
of the Tweedie distribution, see table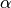 is either
is either- Negative Binomial: the ancillary parameter
alpha, see table - Tweedie: an abbreviation for
 of the power
of the power 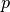 of the variance function, see table
of the variance function, see table
- Negative Binomial: the ancillary parameter
References¶
- Gill, Jeff. 2000. Generalized Linear Models: A Unified Approach. SAGE QASS Series.
- Green, PJ. 1984. “Iteratively reweighted least squares for maximum likelihood estimation, and some robust and resistant alternatives.” Journal of the Royal Statistical Society, Series B, 46, 149-192.
- Hardin, J.W. and Hilbe, J.M. 2007. “Generalized Linear Models and Extensions.” 2nd ed. Stata Press, College Station, TX.
- McCullagh, P. and Nelder, J.A. 1989. “Generalized Linear Models.” 2nd ed. Chapman & Hall, Boca Rotan.
Module Reference¶
Results Class¶
GLMResults(model, params, ...[, cov_type, ...]) |
Class to contain GLM results. |
Families¶
The distribution families currently implemented are
Family(link, variance) |
The parent class for one-parameter exponential families. |
Binomial([link]) |
Binomial exponential family distribution. |
Gamma([link]) |
Gamma exponential family distribution. |
Gaussian([link]) |
Gaussian exponential family distribution. |
InverseGaussian([link]) |
InverseGaussian exponential family. |
NegativeBinomial([link, alpha]) |
Negative Binomial exponential family. |
Poisson([link]) |
Poisson exponential family. |
Tweedie([link, var_power, link_power]) |
Tweedie family. |
Link Functions¶
The link functions currently implemented are the following. Not all link functions are available for each distribution family. The list of available link functions can be obtained by
>>> sm.families.family.<familyname>.links
Link |
A generic link function for one-parameter exponential family. |
CDFLink([dbn]) |
The use the CDF of a scipy.stats distribution |
CLogLog |
The complementary log-log transform |
Log |
The log transform |
Logit |
The logit transform |
NegativeBinomial([alpha]) |
The negative binomial link function |
Power([power]) |
The power transform |
cauchy() |
The Cauchy (standard Cauchy CDF) transform |
cloglog |
The CLogLog transform link function. |
identity() |
The identity transform |
inverse_power() |
The inverse transform |
inverse_squared() |
The inverse squared transform |
log |
The log transform |
logit |
Methods |
nbinom([alpha]) |
The negative binomial link function. |
probit([dbn]) |
The probit (standard normal CDF) transform |


![Var[Y_i|x_i] = \frac{\phi}{w_i} v(\mu_i)](_images/math/ac27ece20bffd63c7eeedfbb655cf3a738bd2120.png)